Pengukur Ketinggian Air Pada Tangki Air / Toren Secara Otomatis Menggunakan ATMEGA8535
By : Unknown
Berikut
adalah listing program lengkapnya:
//kondisi=0
adalah keadaan kosong,
//kondisi=1 adalah keadaan penuh,
//penggunaan variabel kondisi berfungsi sebagai penghilang
//efek bouncing yg disebabkan oleh gelombang air
bit kondisi;
#include <mega16.h>
#define pompa PORTA.0
#define ind_pompa PORTA.5
#define ind_min PORTA.7
#define ind_max PORTA.6
#define mode PINC.0
#define on_off PINC.1
#define maxim PINC.2
#define minim PINC.3
void otomatis()//pemilihan mode otomatis
{
if (mode==1)//mode otomatis
{
if (kondisi==0)
{
if (maxim==1)//kosong
{
pompa=0;
ind_pompa=0;
}
if (maxim==0)//penuh
{
pompa=1;
ind_pompa=1;
kondisi=1;
}
}
if (kondisi==1)
{
if (minim==1)
{
kondisi=0;
}
}
}
}
void manual()//pemilihan mode manual
{
if (mode==0)//manual
{
if (maxim==0)
{
pompa=1;
ind_pompa=1;
}
else
{
if (on_off==0)
{
pompa=0;
ind_pompa=0;
}
else
{
pompa=1;
ind_pompa=1;
}
}
}
}
void indikator()//menyalakan indikator LED MIN dan MAX
{
if (maxim==0) ind_max=0;
else ind_max=1;
if (minim==0) ind_min=0;
else ind_min=1;
}
void main(void)
{
DDRA=0xff; //inisialisasi port mikro
PORTA=0xff;
DDRC=0×00;
PORTC=0xff;
while (1)
{
otomatis();
manual();
indikator();
};
}
//kondisi=1 adalah keadaan penuh,
//penggunaan variabel kondisi berfungsi sebagai penghilang
//efek bouncing yg disebabkan oleh gelombang air
bit kondisi;
#include <mega16.h>
#define pompa PORTA.0
#define ind_pompa PORTA.5
#define ind_min PORTA.7
#define ind_max PORTA.6
#define mode PINC.0
#define on_off PINC.1
#define maxim PINC.2
#define minim PINC.3
void otomatis()//pemilihan mode otomatis
{
if (mode==1)//mode otomatis
{
if (kondisi==0)
{
if (maxim==1)//kosong
{
pompa=0;
ind_pompa=0;
}
if (maxim==0)//penuh
{
pompa=1;
ind_pompa=1;
kondisi=1;
}
}
if (kondisi==1)
{
if (minim==1)
{
kondisi=0;
}
}
}
}
void manual()//pemilihan mode manual
{
if (mode==0)//manual
{
if (maxim==0)
{
pompa=1;
ind_pompa=1;
}
else
{
if (on_off==0)
{
pompa=0;
ind_pompa=0;
}
else
{
pompa=1;
ind_pompa=1;
}
}
}
}
void indikator()//menyalakan indikator LED MIN dan MAX
{
if (maxim==0) ind_max=0;
else ind_max=1;
if (minim==0) ind_min=0;
else ind_min=1;
}
void main(void)
{
DDRA=0xff; //inisialisasi port mikro
PORTA=0xff;
DDRC=0×00;
PORTC=0xff;
while (1)
{
otomatis();
manual();
indikator();
};
}
Flowchart pengukur ketinggian air pada tangki air / toren
By : Unknown
Nama:
FIKRI PRAWOTO
NPM:
14414219
Kelas:
3IB05
Gambar
dibawah adalah gambar tangki air / toren pada saat air dalam keadaan tinggi (High)
atau rendah (Low)
Flowchart
pengukur ketinggian air pada tangki air / toren
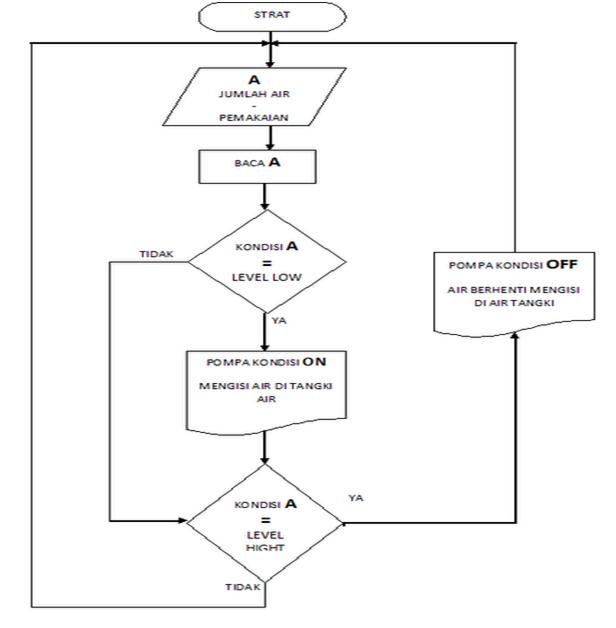
- Pertama saat air berada di bawah (level low)
maka dua pemberat (sinker) akan menggantung dan menarik switch yang
ada pada switch body di bagian atas. Pada saat kondisi
awal, sistem ini akan membaca banyaknya air di dalam tangki.
- Kedua bila banyaknya air berada di
bawah (level low) maka, Switch yang tertarik pemberat
akan membuat kontak relay menjadi close dan
arus listrik akan mengalir melalui kabel menuju mesin pompa air dan
kemudian menyalakannya (start) dan mengisi air ke dalam
toren hingga mencapai level high.
- Ketiga saat air mendekati level high,
maka pemberat bagian bawah akan mengapung dan saat level air mencapai
setengah dari pemberat bagian atas maka level switch akan
kembali ke posisi awal (dengan bantuan pegas yang ada dalam switch
body) sehingga kontak relay akan menjadi open dan
arus listrik terputus sehingga mesin pompa air berhenti (stop) secara
otomatis.
- Keempat batas level high dan
level low dalam toren ini dapat di-setting sesuai
keinginan, dengan mengatur ketinggian dari dua pemberat ini. Cukup dengan
mengatur panjang talinya dan kemudian dikencangkan kembali ikatannya.
- Kelima Jika setting level low-nya
dinaikkan (pemberat bagian bawah posisnya lebih naik), maka volume air
dalam toren akan masih tersisa banyak sesaat sebelum air diisikan kembali.
Begitu pula jika setting level high-nya
dinaikkan (dengan menaikkan lagi posisi pemberat bagian atas), maka volume
air akan bisa mendekati maksimum kapasitas yang bisa ditampung dalam toren
sesaat setelah mesin air dimatikan.
- Keenam bila jarak antara kedua
pemberat sangat pendek (sehingga jarak level low dan high berdekatan)
maka akibatnya interval pengisian air akan lebih singkat sehingga mesin
pompa air akan semakin sering start-stop. Apalagi jika toren
yang digunakan memiliki kapasitas kecil, misalnya 500 liter. Ingat, start mesin
pompa air akan menyerap daya listrik yang cukup besar. Karena itu setting pemberat
ini lebih disesuaikan pada kebutuhan dengan pertimbangan aspek volume
cadangan air dalam toren dan penghematan daya listrik.
SUMBER
:
Contoh IRR Dan NPV
By : Unknown
IRR
Contoh 1:
Sebuah proyek ini diharapkan memiliki
Net Present Value dari $ 865 pada tingkat diskonto 20% dan NPV negatif dari $
1.040 pada tingkat diskonto 22%. Hitung IRR.
Penyelesaian:
Jarak antara 2 NPV = 865 + 1040 = $
1.905
IRR = + 20% (865 / 1905) * (22% - 20%) =
20,91%
Contoh 2:
Informasi berikut berhubungan dengan
proyek investasi Venture Ltd:
Net Present Value (NPV) dengan biaya 25%
dari modal: $ 1.714
NPV pada biaya 30% dari modal: ($ 2937)
Hitung Internal Rate of Return.
Penyelesaian:
Jarak antara 2 NPV = 1714 + 2937 = $
4.651
IRR = + 25% (1714 / 4651) * (30% - 25%)
= 26,84%
Jika IRR lebih besar dari biaya modal,
terima proyek tersebut.
Jika IRR kurang dari biaya modal, tolak
proyek tersebut.
NPV
A pada hari ini mendapat pinjaman dari B
sebanyak Rp 100 juta yang ingin saya investasikan selama satu tahun. Ada 3
pilihan bagi saya untuk menanamkan uang saya tersebut, yaitu :
1. Deposito 12 bulan dengan bunga
8%/thn,
2. Beli rumah lalu dikontrakkan Rp 10
jt/thn untuk kemudian semoga bisa dijual di akhir tahun dengan harga Rp 150
juta,
3. Beli emas sekarang dan dijual akhir
tahun.
Agar dapat lebih mudah memilih investasi
yang paling menguntungkan, A ingin tahu berapa sih nilai sekarang dari hasil
investasi untuk masing-masing pilihan? Atau dengan kata lain, berapa rupiahkan
uang yang akan A terima dari masing-masing pilihan investasi seandainya hasil
investasi tsb A terima sekarang, bukannya satu tahun kedepan?NPV digunakan
untuk menjawab pertanyaan ini.
NPV merupakan hasil penjumlahan PV
pengeluaran untuk investasi dan PV penerimaan dari hasil investasi.
Rumus untuk menghitung Present Value
adalah :
PV = C1 / (1 + r)
Dimana C1 = Uang yang akan diterima di
tahun ke-1.
r = Discount rate/ opportunity cost of
capital.
Tingkat pengembalian/hasil investasi (%)
dari investasi yang sebanding.
Sedangkan rumus untuk menghitung NPV
adalah :
NPV = C0 + ( C1 / (1 + r))
Dimana C0 = Jumlah uang yang
diinvestasikan (karena ini adalah pengeluaran, maka menggunakan bilangan
negatif).
Untuk menghitung NPV Deposito, saya
menggunakan discount rate (r) sebesar 4 %. Angka ini saya ambil dari tingkat
bunga tabungan.
Jadi ,
NPV Deposito = (-100 jt) + (108 jt / ( 1
+ 0,04 ))
= (- 100 juta) + 103,85 juta
= 3,85 juta
Lumayan juga nih hasilnya.
Untuk menghitung NPV Rumah, saya gunakan
discount rate 12 % untuk mengakomodasi tingkat risiko.
NPV Rumah = (- 100 jt + 10 jt) + (150 jt
/ ( 1 + 0,12))
= ( - 90 jt) + 133,93 jt
= 43,93 jt
Wow, makin kaya aja keliatannya.
Untuk menghitung NPV Emas, discount
rate-nya 0 %, karena emas meskipun berfungsi sebagai store of value / alat
penyimpan kekayaan, emas tidak memberikan hasil.
NPV Emas = (- 100 jt) + ( 100 Jt / (1 +
0,00))
= 0 jt
Untuk berikutnya mari ita coba
menghitung harga emas 10 tahun kemudian:
Harga Oktober 1998 adalah USD 300/oz dan
harga Oktober 2008 adalah USD 900/oz.
Dengan penghitungan sederhana, saya
peroleh rata-rata kenaikan harga emas adalah 20%/thn.
Jadi penghitungan ulang untuk NPV Emas
adalah :
NPV Emas = ( -100 jt) + (120 jt /
(1+0,00))
= (- 100 jt) + 120 jt
= 20 jt
Sumber :
Ekuivalensi
By : Unknown
Konsep Ekuivalensi
Metode ekuivalen adalah metode
mencari kesamaan atau kesetaraan nilai uang untuk waktu yang berbeda. Nilai
Ekivalensi adalah Sejumlah uang pada waktu tertentu dikatakan ekivalen dengan
sejumlah uang yang lain pada waktu yang lain, bila nilai nominalnya berbeda,
tetapi nilai efektifnya sama. Suatu rancangan teknis atau rencana investasi
mengandung sejumlah transaksi, baik penerimaan maupun pengeluaran dalam
berbagai bentuk, selama masa pakai atau masa operasi. Semua jenis transaksinya ini
harus diekivalensikan dulu ke salah satu transaksi dasar. Umumnya diubah ke
transaksi sama rata setiap tahun atau transaksi tunggal di awal jangka waktu
analisa.
Dalam
proses ekivalensi nilai ini digunakan MARR (minimum attractive rate of return) sebagai
suku bunga analisa. Besarnya MARR ini tergantung dari: laju inflasi, sukubunga
bank, peluang dan resiko usaha.
Pada nilai ekivalensi istilah-istilah yang
digunakan adalah:
Pv =
Present Value (Nilai Sekarang)
Fv =
Future Value (Nilai yang akan datang)
An =
Anuity
I
= Bunga (i = interest / suku bunga)
N
= Tahun ke-
P0 =
pokok/jumlah uang yg dipinjam/dipinjamkan pada periode waktu
SI =
Simple interest dalam rupiah
A. Present Value (Nilai Sekarang)
Nilai
Sekarang (present value) adalah nilai sekarang dari satu jumlah uang/satu seri
pembayaran yang akan datang, yang dievaluasi dengan suatu tingkat bunga
tertentu. Metode perhitungan PV dapat dirumuskan seperti dibawah ini:
![Rounded Rectangle: PV = FV / [1+i]n](file:///C:/DOCUME~1/ACER/LOCALS~1/Temp/msohtmlclip1/01/clip_image001.gif) dimana:
dimana:
FV
= Nilai yang akan datang;
i
= suku bunga;
n
= jumlah tahun.
Contoh Soal:
Seorang teknisi elektronika membuat tabungan
untuk dia membuat alat baru dalam waktu 5 tahun. Dengan memperhatikan suku
bunga 15% berapa jumlah uang yang harus ia tabung agar memdapatkan uang sebesar
Rp.80.000.000,-?
Penyelesaian:
PV = FV / [1+i]n
PV = 80.000.000 / [1+15%]5
PV = 80.000.000 / 2,011
PV = Rp 160.908.575,-
B. Future Value (Nilai yang akan datang)
Future
value (terminal value) adalah nilai uang yang akan datang dari satu jumlah uang
atau suatu seri pembayaran pada waktu sekarang, yg dievaluasi dengan suatu
tingkat bunga tertentu. Metode prhitungan FV dapat dirumuskan seperti dibawah
ini
![Rounded Rectangle: FV = PV / [1+i]n](file:///C:/DOCUME~1/ACER/LOCALS~1/Temp/msohtmlclip1/01/clip_image002.gif) |
dimana:
PV = Nilai
sekarang
i
= suku bunga
n
= jumlah tahun
Contoh soal:
Profesor Agasa memperhitungkan 10 tahun
kedepan dana yang ada untuk penelitiannya. Apabila ia menginvestasikan uangnya
saat ini dengan tingkat suku bunga sebesar 15%. Berapa uang yang ia punya
kedepannya dengan investasi awal Rp 50.000.000,-?
Penyelesaian:
FV = PV [1+i]n
FV = 50.000.000 [1+15%]10
FV = 50.000.000 [ 4,045]
FV = Rp 202.277.886,-
C. Annuity
Annuity adalah suatu rangkaian pembayaran uang
dalam jumlah yang sama yang terjadi dalam periode waktu tertentu. Annuity dapat
dibagi menjadi dua yaitu annuity nilai sekarang dan annuity nilai masa datang.
Anuitas nilai sekarang adalah sebagai nilai
anuitas majemuk saat ini dengan pembayaran atau penerimaan periodik dan sebagai
jangka waktu anuitas.
Anuitas nilai masa datang adalah sebagai nilai
anuaitas majemuk masa depan dengan pembayaran atau penerimaan periodik dan n
sebagai jangka waktu anuitas.
Dimana A merupakan pembayaran atau pembayaran
setiap periode (Annuity)
Contoh
soal:
Seorang pelajar mengidentifikasi teknologi 4G
yang dapat dikembangkan lagi agar menjadi lebih cepat. Alat itu membutuhkan
dana sebesar Rp 20.000.000,- yang dapat diangsur 15 tahun. Dengan suku bunga
10% berapa uang yang ia sediakan setiap tahunnya?
Penyelesaian:
Penyelesaian:
FV = A [(1+i)n-1] / i
A = [FV] [i] / [(1+i)n-1]
A = [20.000.000] [10%] / [(1+10%)15-1]
A = [2.000.000] / [3,177]
A= Rp 629.525,-
D. Bunga (Interest)
Bunga
adalah uang yang dibayarkan atau dihasilkan dari penggunaan uang. Bunga dapat
dibagi menjadi dua yaitu Simple Interest dan Compound Interest. Simple Ineterst / SI (Bunga
Sederhana) adalah bunga yang dibayarkan/dihasilkan hanya dari jumlah uang
mula-mula atau pokok pinjaman yang dipinjamkan atau dipinjam. Dapat dituliskan:
Contoh soal:
Rendi adalah mahasiswa yang menginvestasikan
uangnnya untuk keperluan kuliah selama 4 tahun. Jika ia berinvestasi sebesar
Rp.400.000,- dengan suku bunga sebesar 10%, berapakah bunga yang akan didapat
mahasiswa tersebut?
Penyelesaian:
SI = Po (i) (n)
SI = 400.000 (10%) (4)
SI = Rp 160.000,-
Compound Interest (Bungan Berbunga) Adalah
bunga yang dibayarkan/dihasilkan dari bunga yang dihasilkan sebelumnya, sama
seperti pokok yang dipinjam/dipinjamkan.
E. Waktu dan Investasi Awal
Istilah
lainnya yaitu n menunjukan waktu dalam rumusan perhitungan present value,
future value, interest, maupun annuity. Waktu ini sangat penting karena
menyangkut lamanya investasi berjalan dan sebagai acuan untuk perhitungan
keuntungan dari hasil investasi tersebut.
Contoh soal:
Seorang pengusaha menginvestasikan uangnya
sebesar Rp.20.000.000,- jika pengusaha tersebut menginginkan agar uangnya
menjadi Rp.62.116.000,- berapa lama ia harus menginvestasikan uangnya dengan
mempertimbangkan suku bunga sebesar 12% ?
Penyelesaian:
Dalam hal ini kita dapat menggunakan rumus
future value:
FV = PV [1+i]n
62.116.000 = 20.000.000 [1+12%]n
3,1083 = [1,12]n
n = 1,12log 3,1083
n = 10
jadi
pengusaha tersebut harus menginvestasikan uangnya selama 10 tahun untuk
mendapatkan hasil yang diinginkan. Istilah berikutnya adalah Po atau investasi
awal. Investasi awal akan sangat menentukan hasil dari investasi yang kelak
akan didapatkan. Untuk menentukan investasi awal juga perlu memperhatikan suku
bunga dan lamanya waktu berinvestasi. Dalam rumus perhitungan, Po biasanya akan
dihitung bersamaan untuk menentukan bunga sederhana atau Simple Interest.
Contoh soal:
Seseorang mendapatkan bunga sebesar Rp
1.000.000,- dari hasil investasinya. Dengan suku bunga sebesar 10% dan waktu
insesatasi selama 8 tahun, tentukanlah investasi awal yang diberikan oleh orang
tersebut?
Penyelesaian:
SI = Po [i] [n]
1.000.000 = Po [10%] [8]
Po = 1.000.000 / 0,8
Po = Rp 1.250.000,-
Contoh Ekivalensi Nilai Tahunan
CV “Mandiri” memerlukan sebuah mesin dengan
spesifikasi teknis tertentu. Ada 2 alternatif pompa yang memenuhi persyaratan
yaitu mesin X dan mesin Y, dengan data-data sebagai berikut:
Bila MARR= 20% per tahun, mesin yang mana yang
sebaiknya dipilih?
Penyelesaian:
- Mesin X :
P=400jt, Fsisa = 200jt, n= 8 thn, A= 90jt,
i=20%
Ax = P (A/P,i%,n) + A – Fsisa(A/F,i%,n)
Ax = 400jt (A/P,20%,8) + 90jt – 200jt
(A/F,20%,8)
Ax = 400jt (0,26061 ) + 90 jt – 200jt
(0,06061)
Ax = 104.244.000 + 90.000.000 –12.122.000
Ax = Rp. 182.122.000
- Mesin Y :
P = 700jt, Fsisa = 400jt, A= 40jt, n=12, i=20%
Ay = P (A/P,i%,n) + A – Fsisa(A/F,i%,n)
Ay = P (A/P,20%,12) + A – Fsisa(A/F,20%,12)
Ay = 700 juta x 0,22526 + 40 juta - 400 juta x
0,02526
Ay =157.682.000 + 40.000.000 –10.104.000
Ay = 187.578.000
Keputusan :
Perbandingan EUAC :
Mesin X : Rp 182.122.000
Mesin Y : Rp. 187.578.000
Pilih Mesin X karena biayanya lebih murah.
Contoh Ekivalen Nilai Sekarang
PT. Telkom sedang mempertimbangkan keputusan
untuk membeli alat Sistem Kontrol Telepon (kapasitas 1000 lines). Ada 3 vendor
yang menawarkan alat tsb yaitu ATT, EWSD, NEAX. Jika diketahui MARR = 20%,
vendor manakah yang sebaiknya dipilih? Karaketeriistik biaya alat dari ketiga
Vendor tersebut adalah sebagai berikut (dalam ribuan US$):
Diketahui :
ATT : Pawal = 1.250.000 , A=40.000,F= 125.000
EWSD : Pawal = 1,1juta, A= 50.000, F= 110.000
NEAX : Pawal = 1 juta, A=60.000, F=100.000
i=20%, n = 15
Ditanyakan :
Vendor manakah yang sebaiknya dipilih?
Penyelesaian :
Vendor ATT :
PW = Pawal + A(P/A,20%,15) – F (P/F,20%,15)
PW = $1.250.000+40.000(P/A,20%,15) –
125.000(P/F,20%,15)
P = $1.250.000+40.000(5,8474)-125.000 (0,1229)
P = $1.468.534
Vendor EWSD :
PW = Pawal + A(P/A,20%,15) – F (P/F,20%,15)
PW = $1.100.000+50.000(P/A,20%,15) – 110.000
(P/F,20%,15)
P = $1.100.000+50.000(5.8474)-110.000(0,1229)
P = $1.378.581
Vendor NEAX:
PW = Pawal + A(P/A,20%,15) – F (P/F,20%,15)
PW = $1.000.000+60.000(P/A,20%,15) – 100.000
(P/F,20%,15)
P = $1.000.000+60.000(5,8474)-100.000(0,1229)
P = $1.338.554
Keputusan :
Minimize Cost -> Pilih Vendor NEAX
Sumber:



